Enter the stress in the x direction, stress in the y direction, and shear stress into the calculator to determine the principal stresses.
Principal Stress Formula
The following formula i used to calculate the two principal stresses.
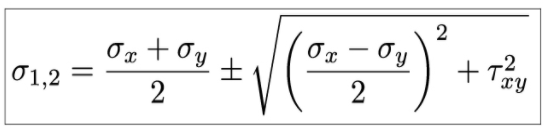
- Where σ1,2 are the principal stresses
- σx is the stress in the x direction
- σy is the stress in the y direction
- τ is the shear stress
Principal Stress Definition
Principal stress are defined as the maximum and minimum total stresses acting on an object at any given point.
Principal Stress Example
How to calculate a principal stress?
- First, determine the normal stress.
Calculate the normal stress in the x and y directions along the plane of action.
- Next, determine the shear stress.
Calculate the shear stress in the x-y plane.
- Finally, calculate the principal stresses.
Calculate the principal stress (max and min) using the equation above.
FAQ
What is a principal stress?
A principal stress is defined as the normal stress calculated at an angle where the shear stress in the plane is 0.
Related Terms
| principal stress calculator |
| principal stress formula |
| principal stress |
| how to calculate a principal stress |
| maximum principal stress |
| stress transformation equations |
| principal stress definition |
| max principal stress |
| major principal stress |
| 1st principal stress |
| maximum normal stress formula |
| shear stress on principal plane is |
| principal plane and principal stress |
| principal plane is a plane on which the shear stress is |
| define principal stress |
| stress transformation calculator |
| principal shear stress |
| 3d principal stress calculator |
| principal stress formula 3d |
| maximum shear stress calculator |
| normal and shear stress on a plane |
| how to find principal stresses |
| minimum principal stress |
| principal strain equation |
| principal strain calculator |
| calculating principal stresses from stress tensor |
| principal stress example |
| principal stress direction |
| define principal plane and principal stress |
| major and minor principal stress |
| minor principal stress |
| intermediate principal stress |
| determine the principal stresses |
| max in plane shear stress |
| maximum principal stress theory formula |
| 3d principal stress |
| the shear stress on the principal plane is |
| how to calculate principal stresses |
| von mises stress calculator 3d |
| principal stress meaning |
| principal plane stress |
| principal normal stress |
| first principle stress |
| 2nd principal stress |
| maximum and minimum principal stress |
| three principal stresses |
| finding principal stresses |
| principal stress angle |
| principle of stress |
| principal plane formula |
| shear stress on principal plane |
| define principal stress and principal plane |
| principle of shear stress |
| 3d stress transformation calculator |
| principal tensile stress |
| cauchy stress principle |
| pure shear principal stress |
| normal stress on the plane of maximum shear |
| formula of principal stress |
| stress transformation equations derivation |
| difference between von mises and principal stress |
| principal stress and strain formula |
| middle principal stress |
| how to find principal stresses using mohr’s circle |
| max and min principal stress |
| max principal stress abaqus |
| principal stress and maximum shear stress |
| maximum shear stress plane |
| maximum in plane shear stress calculator |
| orientation of principal stress |
| principal stresses under a given loading |
| maximum principal stress ansys |
| principal stress equation 3d |
| maximum principal stress definition |
| difference between normal stress and principal stress |
| principal stress matrix |
| min principal stress |
| 2d principal stress |
| principal plane and stress |
| principal stresses and principal planes ppt |
| maximum normal stress equation |
| how to determine principal stresses |
| maximum shear stress from principal stresses |
| normal stress on oblique plane |
| von mises stress principal stress |
| principal stresses and maximum shear stress |
| significance of principal stress |
| principal stress ppt |
| principal deviatoric stress |
| principal plane and principal stress definition |