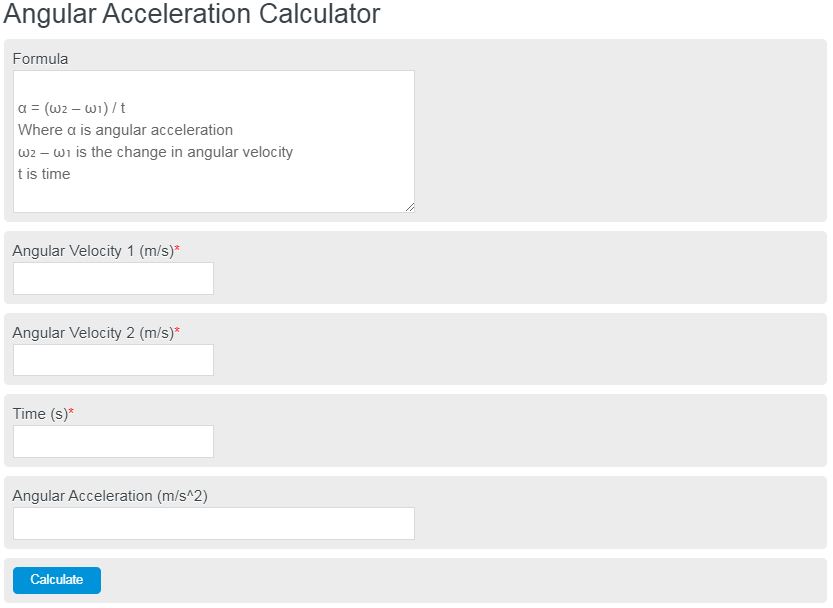
Calculate the angular acceleration of an object. Enter the initial angular velocity, final angular velocity, time, and radius to calculate the angular acceleration.
- Angular Velocity Calculator
- Acceleration Calculator
- Velocity Calculator
- Angular Frequency Calculator
- Centripetal Force Calculator
- Tangential Acceleration Calculator
Angular Acceleration Formula
The formula for calculating the angular acceleration of an object in circular motion is as follows:
α = (ω₂ - ω₁) / t
- Where α is the angular acceleration
- ω₂ – ω₁ is the change in angular velocity
- t is time
Angular acceleration can also be calculated through the following equation:
α = a / R
- Where α is the angular acceleration
- a is the tangential acceleration
- R is radius
To calculate the angular acceleration, divide the tangential acceleration by the radius of rotation.
Angular Acceleration Definition
Angular acceleration is the rate of change of velocity in an object that is undergoing a circular rotation. Specifically, this is the change in angular velocity, not the change in tangential velocity, although it can be calculated from that as well.
How to calculate angular acceleration
To calculate the angular acceleration of an object you first need to calculate its angular velocity. This can be done through this calculator. Next, you need to measure the total time that passes. Finally, you need to measure and calculate the final angular velocity. Enter all of these values into the calculator above and you have your answer.
The last step in this process is to analyze your result to see if it makes sense. When calculating problems in physics, one of the best ways to ensure accuracy is to think about the answer and see if it makes logical sense. If your values are 10,000 times what you expected, it’s likely a mistake in your calculations.
FAQ
What is angular acceleration?
Angular acceleration is the rate of change of velocity in an object that is undergoing a circular rotation. Specifically, this is the change in angular velocity, not the change in tangential velocity, although it can be calculated from that as well. Add question