Enter the equation of a plane and the coordinates of a point to calculate the distance from the point to the plane.
- All Distance Calculators
- Distance Between Points Calculator
- Midpoint Calculator
- Arc Length Calculator
Distance from point to plane formula
The following equation can be used to calculate the distance between a plane and a point.
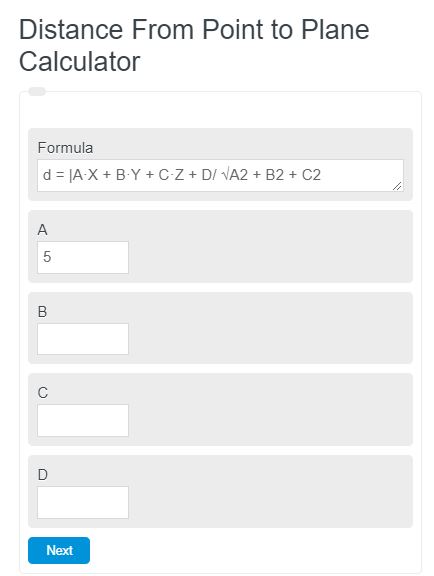
d = |A·X + B·Y + C·Z + D/ √A^2 + B^2 + C^2
- Where D is the distance
- A, B, C, and D are constants of the plane equation
- X, Y, and Z are the coordinate points of the point
Distance From Point to Plane Definition
The distance from a point to a plane is defined as the shortest distance from a single point to any point on a plane.
How to calculate the distance from a point to a plane?
How to calculate the distance from a point to a plane
- First, determine the equation of the plane.
A 3-dimensional plane can be represented using an equation in the form AX + BY + CZ + D.
- Next, gather the constants from the equation in stead 1.
Separate A, B, and C in the equation determined in step 1.
- Next, determine the coordinates of the point
Measure or calculate the coordinates of the points x,y, and z.
- Calculate the distance
Calculate the distance from the point to the plane using the equation above and information from steps 1-3.
FAQ
Great question. The answer to this is that you can only calculate the average distance to the plane which will be a point directly perpendicular to the point and plane.