Enter the annual interest rate and the compounding time period on a loan to calculate the effective annual interest rate of the loan.
EAR Formula
The following formula is used to calculate the effective annual interest rate of a loan.
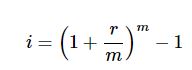
- r is the nominal annual interest rate (%)
- i is the effective annual rate (%)
- m is the number of compounding periods per year
To calculate the effective annual interest rate, add a value of one to the result of the annual rate and divide by the number of compounding periods. Take this result, raise it to a power of the number of compounding periods, then subtract 1 from that result.
EAR Definition
EAR is a financial term that stands for the effective annual rate. EAR is used to describe interest on a loan or mortgage in terms of compounding annual interest rates. In other words, it converts the nominal interest rate to a compounding interest rate.
How to calculate EAR?
The following example is a step-by-step guide to calculating the EAR of a loan.
- The first step in calculating the EAR of a loan is to determine the nominal interest rate on the loan. This is typically provided when agreeing to the terms of a loan. For this example, we will say the interest rate is 3.5% yearly.
- The next step is to determine the compounding periods before the year. Most often, the compounding period is monthly. In other words, there would be 12 compounding periods per year. Sometimes these could be compounding weekly or even daily. Those types of terms need to be looked out for when agreeing to a loan. For this example, we will say the compounding period is the typical monthly period.
- The final step is to plug these values into the formula above and solve. You may also simply plug the values into the calculator above, and we find the effect annual rate to be 3.556%. As you can see not much change with only monthly compounding periods.
FAQ
EAR is used to describe the interest on a loan or mortgage in terms of compounding annual interest rates.