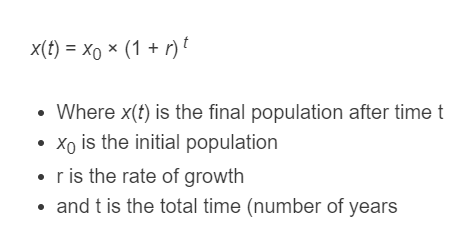Enter the current population, number of years, and growth rate into the population growth calculator. The calculator will display the new population after the number of years entered. If you already know the final population and want to calculate the percent growth, visit the percent growth calculator linked below. Check out our partner for zipcode-related population data.
- Percent Growth Calculator
- Exponent Calculator
- Exponential Growth Calculator
- Population Density Calculator
Population Growth Formula
The following formula is used to calculate a population size after a certain number of years.
x(t) = x0 × (1 + r) t
- Where x(t) is the final population after time t
- x0 is the initial population
- r is the rate of growth
- and t is the total time (number of years)
Population Growth Definition
Population growth is defined as the percentage increase in a population over a given time period.
How to calculate population growth?
Example#1:
First, the initial population must be determined. For this example, the initial population size is estimated to be 10,000.
Next, you must calculate or estimate the growth rate. This is typically a growth rate per year in percent, but it can be any period length the problem calls for.
For this problem, the growth rate is found to be 12% per year.
Next, you must determine the total number of years or periods that the growth occurs for. In this example, the growth occurs for 5 consecutive years.
Finally, the final population amount can be calculated using the formula above.
x(t) = x0 × (1 + r) t
x(t) = 10000 × (1 + .12)5
x(t) = 17958.56
Plugging in the information from the steps above, the final population is calculated to be 17958.56. Sometimes these numbers are rounded to the closest integer because you can have half a person.
Example #2:
In this next problem, we will look at a case in which the population grows on a shorter time scale of a month.
The initial population is given as 10,000. the growth rate is 15% per month, and the length of growth is 20 months.
x(t) = x0 × (1 + r) t
x(t) = 10000 × (1 + .15)20
x(t) = 163,666
Using the same formula as before, the growth of the population is found to be 163,666. In this problem, we can really see the effect of compound growth.
FAQ
Population growth is the increasing growth of a population due to reproducing.
A population growth rate is a rate at which a population increases every year, or per time period that is being analyzed.
Typically population growth is exponential, however, at some point, all populations hit a tipping point where they cant support their growth rate any longer due to many factors including health and food supply.