Enter the semi-major axis of the orbit, the mass of the satellite, and the mass of the central object to determine the orbital period.
- Orbital Speed Calculator
- Roche Limit Calculator
- Rocket Equation Calculator
- Thrust Calculator
- Orbital Acceleration Calculator
- Orbital Distance Calculator
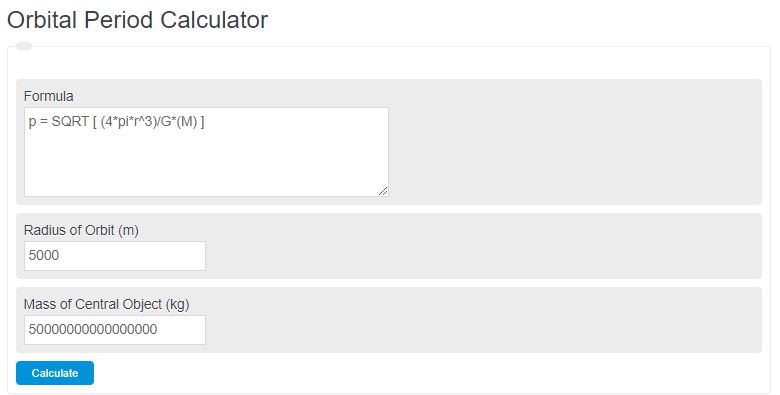
Orbital Period Formula
The following formula is used to calculate the orbital period.
p = SQRT [ (4*pi*r^3)/G*(M) ]
- Where p is the orbital period
- r is the distance between objects
- G is the gravitational constant
- M is the mass of the central object
To calculate the orbital period, multiply the distance cubed by 4 times pi, and divide the result by the result of the gravitational constant times the mass of the center object. Finally, take the square root of the result to get the orbital period.
In the original equation, the mass of the satellite is included as well, but it’s so much smaller than the central object that it’s negligible and can be ignored.
Orbital Period Definition
An orbital period is defined as the total time it takes a satellite or orbiting object to make one complete rotation around another larger object.
Orbital Period Example
How to calculate orbital period?
- First, determine the distance between objects.
Calculate the distance between centers.
- Next, determine the mass of the larger object.
Calculate the mass of the larger object.
- Finally, calculate the orbital period.
Calculate the orbital period using the equation above.
FAQ
An orbital period is a measure of time it takes a smaller body to orbit around another object.
In the case of an ellipse, simply replace the radius between objects with the average of the major and minor axis of the orbit.