Calculate the new coordinates of a point that has rotated about the z-axis of the coordinate plane. Enter the original coordinates and the total rotation to calculate the new coordinates. This calculator can display new coordinates by either clockwise or counter-clockwise rotation.
- Unit Vector Calculator
- Reference Angle Calculator
- Double Angle Calculator
- Polar Coordinates Calculator
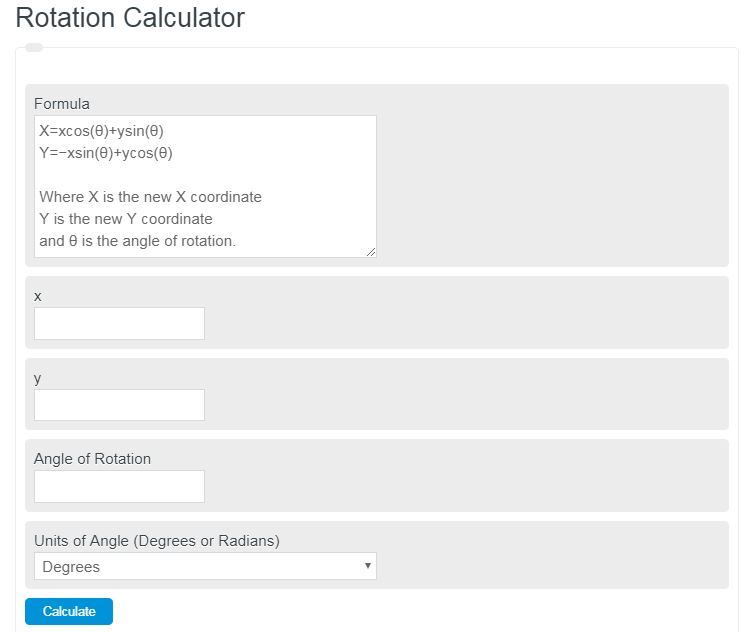
New Coordinates by Rotation Formula
The following formula can be used to calculate the coordinate point in the x-y plane that has rotated by some angle (θ) about the x-axis.
X=xcos(θ)+ysin(θ)
Y=−xsin(θ)+ycos(θ)
- Where X is the new X coordinate
- Y is the new Y coordinate
- and θ is the angle of rotation.
How to calculate the new coordinates of a point that’s rotated about an axis?
Points in the coordinate plane are all governed by trigonometry and the corresponding formulas. This is because a triangle can be drawn by any point by starting at the origin, drawing a straight line to the point, and then a vertical line to the x-axis.
Once you visualize that triangle, you can then understand how the sine and cosine of the angles of that triangle can be used to find the location of the points.
Using that knowledge the equations outlined above can be formulated in calculating the new coordinates of a point that has rotated about the axis at some angle theta.
The following example is a step-by-step guide on using those equations to calculate the new coordinate points.
The first step is finding or determining the original coordinates. This is typically given but can be calculated if needed. For this example, we will say that point is (6,8).
The next step is to determine the angle of rotation, theta. We will say the angle is 45 degrees of clockwise rotation.
The final step is to plug these values into the formulas above to determine the new points. So, X= 9.89, Y=-1.41.
Check your answer using the calculator above.
3 Things to Know About Coordinate Rotation
1. Is rotation a transformation?
Rotation of coordinates to a new location is considered a type of transformation of those points, but transformations are not always a rotation. They can and often are much more complex than rotating points about an axis.
2. Are rotations clockwise or counterclockwise?
Rotations can be both clockwise and counterclockwise, however, the calculator above solves for clockwise rotation.
3. Is rotation and revolution the same?
The terms revolution and rotation are synonomous. One revolution is equal to a rotation of 360 degrees.