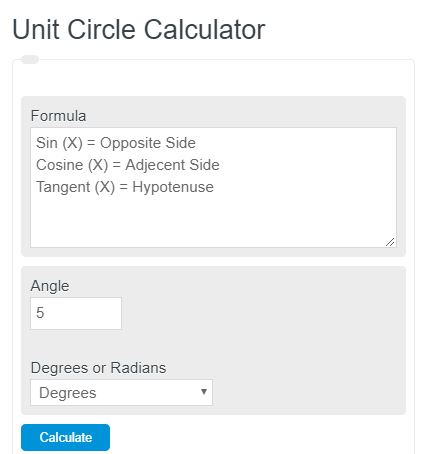
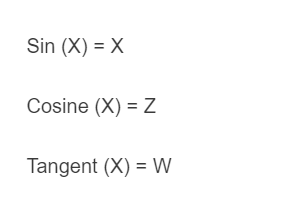Enter the angle of the unit circle into the calculator. The calculator will display the corresponding sine, cosine, and tangent values of the unit circle associated with those values.
- Normalize Vector Calculator
- Cosecant Calculator
- Phasor Calculator
- Resultant Vector Calculator
- Circular Mils Calculator
Unit Circle Formula
The following formula is used to calculate the values of a unit circle.
Sin (X) = X
Cosine (X) = Z
Tangent (X) = W
Where x is the angle and y, z, and w are the values of the unit circle.
To calculate a unit circle, take the sine, cosine, and tangent of the angle to get the X, Y, and Z coordinates, respectively.
Unit Circle Definition
A unit circle is defined as any circle with a radius of 1 unit.
How to memorize a unit circle?
The best way to memorize a unit circle is to remember that sin is X, cosine is y, and tan is z. Add that to the factor that the unit circle always has a radius of 1, and you can determine your unit circle.
What is it called unit circle?
The unit circle is called such because the radius of the circle is a unit of 1, or magnitude of 1. That is one unit, hence the name unit circle.
Why are unit circles important?
Just like with a unit vector, unit circles are important for simplifying problems with large numbers. If you can simply a problem down to a unit circle with a radius of 1, then you can compare the values of circles with drastically different sizes.
How to calculate a unit circle?
How to calculate a unit circle
- First, measure the angle of the unit circle.
This is the angle measured from the positive x axis.
- Calculate the value of sine (X)
This value will be equal to the Y portion of the triangle encapsulated.
- Calculate the value of cosine (X)
This will be equal to the x portion of the triangle.
- Calculate the value of tangent of (X)
This is equal to the value of the hypotenuse.
FAQ
A unit circle is a circle with a radius of 1. It’s also closely related to a unit vector which is a vector with a magnitude of 1, however, it is no the same.
A unit circle is used in order to simplify a problem down to a smaller scale, of 1 to be exact. In other words, it’s reducing a large circle value to one with a radius of 1.