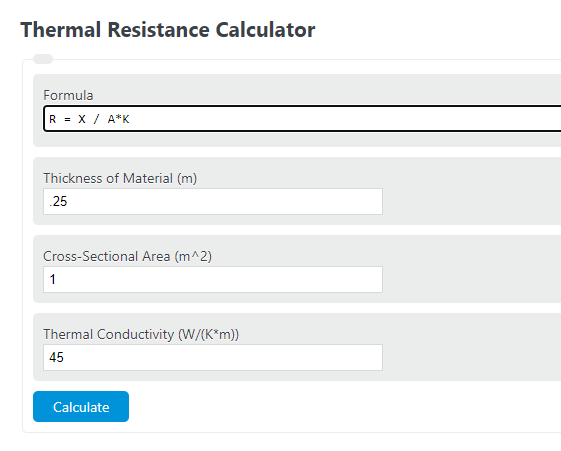
Enter the thickness of the material parallel to heat flow, the thermal conductivity, and the cross-sectional area into the calculator to determine the thermal resistance.
- Conductivity to Resistivity Calculator
- Thermal Energy Calculator
- Thermal Conductivity Calculator (heat flux)
- Final Temperature Calculator
- Resistance to Temperature Calculator
- Armature Resistance Calculator
- Thermal Diffusivity Calculator
Thermal Resistance Formula
The following formula is used to calculate thermal resistance.
R = X / A*K
- Where R is the absolute thermal resistance (K/W)
- X is the thickness of the material parallel to heat flow (m)
- A is the cross-sectional perpendicular to heat flow (m^2)
- K is the thermal conductivity of the material (W/(K*m))
To calculate thermal resistance, divide the thickness of material parallel to heat flow by the cross-section area perpendicular to the heat flow, then multiply by the thermal conductivity.
Thermal Resistance Definition
What is thermal resistance? Thermal resistance is a measure of the rate of change in temperature of a material per unit of energy added to the material. In other words, the resistance to the flow of heat energy.
Example Problem
How to calculate thermal resistance?
- First, determine the thickness of the specimen.
For this example, the thickness of the material that is parallel to heat flow is .25m.
- Next, determine the cross-sectional area.
The heat flow for this problem is moving through a square of 1m x 1m = 1m^2.
- Next, determine the thermal conductivity.
This can typically be found on online tables. The material in this problem is steel which has a thermal conductivity of 45 W/(K*m).
- Finally, calculate the thermal resistance.
Using the formula above, the thermal resistance is calculate as .25 / (1*45) = .0055 (K/W).
About Thermal Resistance
What does thermal resistance depend on? Thermal resistance is dependent on three factors; the thermal conductivity of the material, the thickness of the material parallel to heat flow, and the cross-sectional area perpendicular to heat flow.
Is a higher thermal resistance better? When attempting to insulate an object or structure, a higher thermal resistance is better. However, if you are looking at an application such as a frying pan, you want the thermal resistance to be as low as possible so that as much energy transfers from the burner to the food.
Can a thermal resistance be negative? Thermal resistance cannot be negative. This is because thermal conductivity, thickness, and cross-sectional area can also not be negative. Or in other words, the heat has to go somewhere.